HYDRO_ST-2D 2-dimenziós lebegő-/károsanyag
szállítási modellek
1. Bevezetés
A HYDRO_ST-2D kétdimenziós lebegő-/károsanyag szállítási modell a HYDRO_AS-2D kétdimenziós áramlásmodell bővítését jelenti. Itt az áramlásegyenleteken túlmenően még az anyagkoncentráció, valamint esetleg a mederfenék változásai egyenleteinek (Exner-egyenletek) numerikus megoldása is megtörténik.
2. A lebegő-/károsanyag szállítási modell matematikai-numerikus modellje
A C anyagkoncentráció eloszlása a modelltartományban a következő mélységi átlagolt konvektív-diffúz egyenlettel modellezhető (Lee et al. 1994):
![]()
ahol az egyes mennyiségek:
| Ci | lebegő- / károsanyag-koncentráció [kg/m3], |
|---|---|
| kx und ky | diffúziós együttható x és y irányban [m2/s], |
| Sdi | lerakódási tag [kg/m2s], |
| Sei | eróziós tag [kg/m2s]. |
Ez az egyenlet a lebegőanyag szállítása esetében legfeljebb öt különböző di szemcsenagyságra egyidejűleg megoldható.
Az Sdi lerakódási tag a következő összefüggéssel határozható meg (Lee et al. 1994):
![]()
A wsi effektív süllyedési sebesség többek között közvetlenül a szemcsenagyságtól és a pehelyképződéstől (összefüggő üledék), valamint közvetetten a turbulenciától függ.
A wsi [m/s] (a di szemcsenagyságnál) a programban a következő összefüggéssel számítható:
![]()
ahol a ksi együttható és az msi kitevő nagyban függ kísérleti (helyszínen vagy laborban végzett) meghatározásuktól. Így az irodalom szerint ksi értéke 0,1 mm/s és 200 mm/s, míg msi értéke 0,5 és 2 között szóródik.
Annak pi valószínűsége, hogy a lebegőanyag lerakódik:
![]()
ahol τb = a tényleges fenék-nyírófeszültség [N/m2] és τcdi = a kritikus nyírófeszültség [N/m2] a di szemcsenagyságnál (Lee et al. 1994). A lerakódási tag nullává válik, ha
τb > τcdi (nincs lerakódás).
Az Sei lerakódási tag konszolidált (nem összefüggő) üledékek esetén az alábbi összefüggéssel határozható meg(Ariathurai und Arulanandan 1978,):
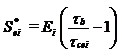
ahol Ei = az eróziós együttható és τcei = a kritikus nyírófeszültség az adott „i“frakció eróziójánál (Lee et al. 1994).
Összefüggő (nem konszolidált) üledékek esetén az Sei eróziós tag az alábbi összefüggéssel határozható meg (Parchure und Mehta 1985):
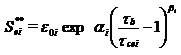
ahol az ε0i , αi és βi együtthatók, ill. kitevők az adott frakció eróziós képességét tükrözik vissza.
Az eróziós tag nullává válik, ha τb < τcei (nincs erózió).
A fenti konvektív-diffúz egyenlet megoldása a HYDRO_AS-2D felhasználói kézikönyvének 3. fejezetében leírt módszerrel numerikusan történt.
2.1 Peremfeltételek
A numerikus szimuláció peremfeltételei az alábbiak:
- A bemeneti szélen a teljes anyagbehordást [kg/s] egy menetvonal formájában kell meghatározni. Az anyagkoncentráció keresztmetszet mentén történő egyenletes eloszlása van ekkor feltételezve.
- A lebegő-/károsanyag zavartalanul, ill. szabadon távozhat a kimeneti szélen a modellterületről.
2.2 Mederfenék változásai
A mederfenék üledék-lerakódás és –erózió következtében létrejövő változásai az Exner-egyenlet segítségével modellezhetők:
![]()
ahol ρs = az üledék sűrűségét és np = a meder porozitását jelöli.
3 Alkalmazási terület
A HYDRO_ST-2D-ben jelenleg használt, erózióra vonatkozó képletek a konszolidált (összefüggő) üledék „felületi erózióját” tételezik fel. Ennél is nagyobb vonszoló feszültségeknél (kb. τ > 5 N/m2) úgynevezett „tömeges erózió” következhet be.
Az alkalmazási terület ennél fogva jelenleg elsősorban a növényzettel fedett mentett területekre, valamint tavakra és duzzasztott területekre korlátozódik, ahol kicsik a vonszoló feszültségek (áramlási sebességek).
A túlnyomóan homoktartalmú üledékek lerakódási és eróziós folyamatai az alábbi képlettel modellezhetők:
ahol Ci* a lerakódás/erózió (DVWK 2003, WRC Report / Basson and Rooseboom 1997) ún. egyensúlyi koncentrációját és a az illeszkedési paramétert (mean settling depth) jelöli. Az egyensúlyi koncentráció számítására különböző kiindulási pontok vannak (Ackers and White, Van Rijn, különböző „stream power“ egyenletek, stb.). Tervbe van véve, hogy egy következő fejlesztési fázisban ilyen kiindulási feltételeket is beiktassanak. Ezáltal durvább, túlnyomóan homoktartalmú üledékek modellezése is lehetővé válik (lebegő anyagok szállítása folyók – torkolati – szakaszain, duzzasztók átöblítése stb.).
4 irodalom
ATV - DVWK, Arbeitsbericht: Feststofftransportmodelle für Fließgewässer, März 2003.
G. R. Basson and A. Rooseboom (edt.), Dealing with Reservoir Sedimentation, WRC Report No. TT 91/97, Water Research Commission, Pretoria, South Africa.
D. H. Lee, K. W. Bedford and C. J. Yen, Storm and Entrainment Effects on Tributary Sediment Loads, Journal of hydraulic Engineering, January 1994, Vol. 120, No. 1.
A. H. Elliott, Settling of fine sediments in a channel with emergent vegetation, Journal of hydraulic Engineering, August 2000, Vol. 126, No. 8.
A. P. Nicholas und D. E. Walling, Modelling flood hydraulics and overbank deposition on river floodplains, Earth Surface Processes and Landforms, Volume: 22, Issue: 1, Date: 1997, Pages: 59-77.
B. Gomez, J. D. Phillips, F. J. Magilligan and L. A. James, Floodplain sedimentation and sensitivity: Summer 1993 flood, upper Mississippi river valley, Earth surface Processes and Landforms, Vol. 22, 923–936 (1997).
A. P. Nicholas, Modelling and monitoring flow and suspended sediment transport in lowland river floodplain environments, Department of Geography, University of Exeter, Exeter, Devon, EX4 4RJ, UK (unpublished yet).
Nujic, M., 2005; Flussraumagenda Tiroler Achen (EU Projekt Interreg IIIb), Teilprojekt: Hydraulische und fluss-morphologische Untersuchung zur künftigen Entwicklung des Deltabereichs der Tiroler Achen / Chiemsee, Projektbericht.
Nujic, M., 2005; SUMAD- Sustainable use and management of alluvial plains in diked river areas (EU Projekt); Schwebstoffverlandung in den Donauvorländern unterhalb der Staustufe Vohburg, Projektbericht.
A. Paquier and S. R. Khodashenas, River beddeformation calculated from boundary shear stress (Déformation d ’un lit de rivière calculée à partir de la contrainte de Cisaillement), Cemagref,Hydrology-Hydraulics Research, Unit,CP 220, 69336 Lyon Cedex 09,France.
T. Fischer-Antze, T. Stoesse, P. Bates and N. Olsen, 3d numerical modelling of open-channel flow with submerged vegetation, J.Hydr. Research, Vol. 39, No.3, 2001.
U.S. Army Corps of Engeneering, User Manual TABS MD.

